Olasılık ağacı

İçinde temel olasılık , bir olasılık ağaç bilerek rastgele deney özetlemek için izin veren bir diyagramdır şartlı olasılık .

Bu ağaçlar karar teorisinde yaygın olarak kullanılmaktadır .

Gerçek bir problem örneği

Petrol sondajı örneği . İzin verin $p$ bilinen bir olasılıkla petrolün varlığını hesapladığımız bir yer olsun .

Bir test yaparsak, bu olasılık hala bilinmeyen bir $q$ değerine düzeltilebilir . Test pahalıdır ancak kuru bir kuyuyu açmayı önleyebilir. Öte yandan, testin başarısı, kuyunun kuru olmayacağı kesin olarak anlamına gelmez.

Testi yapmalı mıyız? Testi yapmadan sondaj yapmalı mıyız?

Deneysel plana bakın , Tek kollu haydut (matematik) .

Başka bir örnek

Aşağıdaki rastgele deneyi özetlemeye çalışıyoruz:

Bir zar atıyoruz

Elde edilen sayı 3'ün katı ise, 3 siyah top, 4 beyaz top ve 3 kırmızı top içeren 1. torbadan rastgele bir top çıkarırız
Elde edilen sayı 3'ün katı değilse, 3 siyah top ve 2 beyaz top içeren 2. torbadan bir top çıkarılır.

İlk adım, bir evren tanımlamayı mümkün kılar $Ω = {1; 2; 3; 4; 5; 6}$ bir eşlenebilirlik uyguladığımız (kalıbın mükemmel dengelenmiş olduğunu tahmin ediyoruz). Daha sonra iki tamamlayıcı olayı ele alıyoruz

$U 1$ = "fırlatma, 1 numaralı torbada atışa yol açar"
$U 2$ = "fırlatma, 2 numaralı torbaya atışla sonuçlanır"

Bu nedenle $U 1 = {3; 6}$ ve $p ( U 1 ) = 1/3$ sonra $p ( U 2 ) = 2/3$ .

İkinci adımı incelemek için, 1. torbada veya 2. torbada çekim yaptığınızda ne olduğunu incelemelisiniz.

Torba 1'deki çizim bir evren tanımlamayı mümkün kılar Ω 1 = { N ; B ; Aşağıdaki olasılığı uyguladığımız R }
- $p ( N ) = 3/10$
- $p ( B ) = 4/10$
- $p ( R ) = 3/10$ .

Aslında transfer olan

Q 1

ile tanımlanan bir equiprobability arasında (urn 1 rastgele çekilen bir top olası renk evrenini)

Q 1 '= {N- 1 , N- 2 , N- 3 , B 1 , B 2 , B 3 , B 4 , R 1 , R 2 , R 3 }

(1. torbada bulunan topların evreni, burada 1. torbadaki çekilişin olası ve eşlenebilir sonuçları olarak kabul edilir).

Aynı şekilde, 2 numaralı sandıkta çizim yapmak $,$ 3/5 ve 2/5 olasılıkların $Ω 2 = { N , B }$ evrenini tanımlamayı mümkün kılar .

Deneyim daha sonra aşağıdaki ağaçta özetlenir:

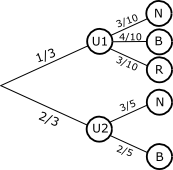
Olasılıkları okumak daha sonra kolayca yapılır:

1. torbada atış yapma ve çeyrek not alma olasılığı:

{\ displaystyle p (U_ {1} \ cap N) = 1/3 \ times 3/10 = 1/10}

2. torbada atış yapma ve çeyrek not alma olasılığı:

{\ displaystyle p (U_ {2} \ cap N) = 2/3 \ times 3/5 = 2/5}

Siyah bir topa vurma olasılığı şu şekildedir:

{\ displaystyle p (N) = p (U_ {1} \ cap N) + p (U_ {2} \ cap N) = 1/2}

Çözülmüş egzersiz

Gerard, A veya B olmak üzere iki yoldan işe koyulabilir. A yolunu izleme olasılığı 0,4'tür. A yoluna girerse, geç kalma olasılığı 0.2'dir. B yoluna girerse, geç kalma olasılığı 0.6'dır. Ya

R

Etkinliği "Gerard geç kaldı" ve

R c

R'nin

tamamlayıcısıdır .

Olasılıkları çıkarıyoruz

"A yolunu izleme olasılığı 0,4'tür." :

P ( A ) = 0,4

. Yalnızca iki olası yol olduğundan,

P ( B ) = 1 - P ( A ) = 0.6'dır

. "A yolunu seçerse, geç kalma olasılığı 0.2'dir." :

P A ( R ), 0.2 =

. A yolunu aldığını bilmenin geç kalmama olasılığı bu nedenle tamamlayıcı

P A ( R c ) = 1 - P A ( R ) = 0.8'dir

. "B yoluna girerse, geç kalma olasılığı 0,6'dır." :

P B ( R ) = 0.6

Aynı şekilde,

P B ( R c ) = 1 - P B ( R ) = 0.4

Tanımlar ve özellikler

Bir olasılık ağacına aşağıdaki kurallara uyan yönlendirilmiş ve ağırlıklı bir grafik diyoruz

Aynı köşeden kaynaklanan dalların ağırlıklarının (veya olasılıklarının) toplamı 1 verir.
Bir yolun olasılığı, onu oluşturan dalların olasılıklarının ürünüdür.
A tepe noktasından B tepe noktasına giden dalın ağırlığı, A'nın halihazırda $p A ( B )$ gerçekleştirildiğini bilen B'nin koşullu olasılığıdır .

Ardından koşullu olasılığın özelliğini buluruz :

p (A \ cap B) = p (A) \ times p_ {A} (B)

(yolların ürünü).

Toplam olasılık formülünün yanı sıra :

Eğer

Q 1

Q 2

, ...,

Ω n

tanımlar bir bölümü

Q

(iki-iki ayrık setleri olan birlik verir

Q'dan

), eğer

Q i

, sıfır olmayan olasılık ve A bir olay olup olmadığını Ω,

p (A) = \ toplam _ {{i = 1}} ^ {n} p (A \ cap \ Omega _ {i}) = \ toplam _ {{i = 1}} ^ {n} p (\ Omega _ {i}) \ kere p _ {{\ Omega _ {i}}} (A)

Örnekte $p$ $($ $N$ $) '$ yi hesaplamak için kullandık

{\ displaystyle p (N) = p (U_ {1}) \ times p_ {U_ {1}} (N) + p (U_ {2}) \ times p_ {U_ {2}} (N)}

p (N) = 1/3 \ times 3/10 + 2/3 \ times 3/5 = 1/2

Olasılık ağacı ayrıca koşullu olasılıkların veya Bayes teoreminin tersine çevrilmesini kolaylaştırır :

p _ {{B}} (A) = {\ frac {p _ {{A}} (B) .p (A)} {p (B)}}

Bir önceki örnekte, bu şu soruyu sormak anlamına gelir: "Bir çeyrek nota attığımızı bildiğimiz halde, 1. sandıkta ateş etme olasılığımız nedir?" "

{\ displaystyle p_ {N} (U_ {1}) = {\ frac {p_ {U_ {1}} (N) \ kere p (U_ {1})} {p (N)}} = {\ frac { 1/10} {1/10 + 2/5}} = 1/5}

Olasılık ağacı

Gerçek bir problem örneği

Başka bir örnek

Çözülmüş egzersiz

Tanımlar ve özellikler

Ayrıca görün

İlgili Makaleler

Dış bağlantılar