Daimi takvim
Bir daimi takvim gösterir herhangi bir tarih için haftanın günü, bu yıl ile sınırlıdır akım takvimine aksine "Herhangi yıl".
Gregoryen ve Jülyen takvimleri için, sürekli bir takvim genellikle üç genel varyasyondan birinden oluşur:
- 14 bir yıllık takvim ve ayrıca belirli bir yıl için hangi bir yıllık takvimin kullanılması gerektiğini gösteren bir tablo. Bu bir yıllık takvimler ayrıca yedi takvimlik iki gruba ayrılır: her ortak yıl için yedi (29 Şubat olmayan yıl), yedi takvimin her biri haftanın farklı bir gününde başlar ve her yıl için yedi takvim. yine her biri haftanın farklı bir gününden başlayarak toplam ondört. (14 takvim için ortak bir adlandırma şeması için Pazar mektubuna bakın.)
- Yedi adet bir aylık (31 günlük) takvim (veya toplam 28 adet olmak üzere 28 ila 31 gün arasında her ayın yedisi) ve belirli bir ay için hangi takvimin kullanıldığını gösteren bir veya daha fazla tablo. Bazı daimi takvimlerin tabloları birbirine karşı kayar, böylece iki ölçeği üst üste hizalamak, belirli bir aylık takvimi bir işaretçi veya pencere mekanizması aracılığıyla ortaya çıkarır. [1] Yedi takvim, yalnızca yedi tanesinin gösterildiği 13 sütunla veya haftanın hareketli günü adlarıyla (cep sonsuz takviminin resminde gösterildiği gibi) tek bir takvimde birleştirilebilir.
- Yukarıdaki iki varyasyonun bir karışımı - gerektiğinde değiştirilebilen hareketli parçalar üzerinde ayların adlarının sabitlendiği ve haftanın günlerinin ve tarihlerin işaretlendiği bir yıllık bir takvim.
Böyle sürekli bir takvim, tropik yıl ve ay döngülerinin bir kombinasyonu temelinde hesaplanan Paskalya gibi hareketli festivallerin tarihlerini göstermez. Bu konular Computus'ta ayrıntılı olarak ele alınmaktadır.
Nürnberger Handschrift GNM 3227a, pratik kullanım için bir sonsuz takvimin ilk örneğidir. Takvim, 1390'dan 1495'e kadar olan dönemi kapsar (bu nedenle el yazması 1389 civarındadır). Bu dönemin her yılı için Noel Günü ile Quinquagesima arasındaki haftaların sayısını listeler. Bu, 15. yüzyılda popüler hale gelen hareketli festivallerin hesaplanmasına izin veren bir sürekli takvimin tablo biçiminin bilinen ilk örneğidir.
GD Moret'in sonsuz takvimi
Bu takvim, sırasıyla yüzyıl, yıl, ay ve tarihin (ayın günü) seçildiği bir dizi üç tablodan oluşur. 0'dan 6'ya kadar (veya 7 olasılık) haftanın gününe karşılık gelen bir sayı elde ederiz.
Tablo versiyonu
ManuelÜç aşamada ilerlemek gerekir:
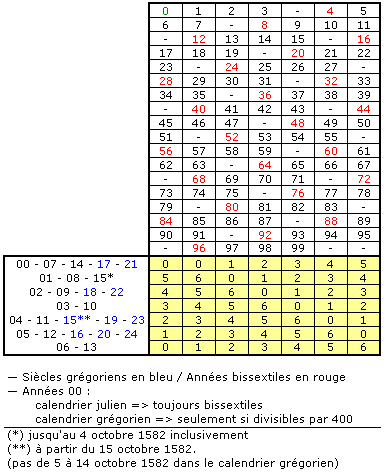
- Tablo 1'de yüzlerce (vintage) ve yılın kesişimindeki sayıyı bulun. "A" sayısı denir. (Bu sayı 0, 1, 2, 3, 4, 5, 6 olabilir). Bu tabloda bir hata kaydı: İlk satır ve ilk sütunun (örneğin 1790 yılı) numarası 0 (sıfır) olarak belirtilir, ancak 6 (altı) olmalıdır. İkna olmak için şu 4 tarihin gününü hesaplamak yeterlidir: 31/12/1789 & 01/01/1790, 12/31/1790 & 01/01/1791.
- Tablo 2'de A satırı ile ay sütununun kesiştiği noktadaki sayıyı bulun. "B" sayısı denir. Bunu yapmak için, 1. adımda elde edilen "A" sayısını kullanarak sol sütundan başlayın (Elde edilen ikinci sayı: 0, 1, 2, 3, 4, 5, 6 olabilir).
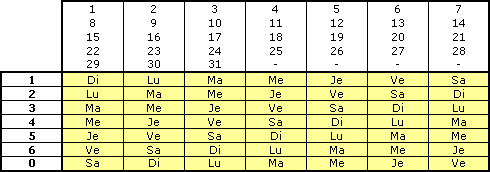
- Tablo 3'te B doğrusu ile aranan tarihin kesiştiği günü bulunuz. Bunu yapmak için, 2. adımdan elde edilen "B" sayısını kullanarak sol sütundan başlayın.
 Tablo 2
ay
Tablo 2
ay

Ezberlenebilir versiyon
Aşağıda önerilen yöntem, Moret takviminin ezberlenebilir bir versiyonudur: mantık ve zihinsel aritmetik kullanarak tabloları kaldırır veya basitleştirir.
Bu yöntem yüzyıla, yıla, aya ve tarihe bir sayı atar. Dört sayıyı toplayarak haftanın gününü elde ederiz. Bu yöntemi ters hesaplamalar yapmak için de kullanabiliriz: Hangi aylar 13'üncü Cuma'yı içerir? Aynı tarihleri kaç yıl sonra bulacağız?
Tüm bu sayılar modulo 7 olarak tanımlanır , yani 5, 12, 19, 26'ya eşittir… Toplama işleminin nihai sonucu haftanın gününü verir, Pazartesi günü 1 sayısını verir. 12 veya -2'nin sonu. bu nedenle örneğin 5'e, yani Cuma'ya tekabül edecektir.
laik numara
"Laik sayı" aynı iki rakamla başlayan tüm yıllar için aynıdır. Resmen bir parçası olmayacaktır rağmen nedenle 2099 2001 2000 yılına bağlantılı XXI inci yüzyılın . Jülyen takviminde ve Gregoryen takviminde hesaplama farklıdır (Fransa dışında Jülyen takviminden Gregoryen takvimine geçiş tarihleri için bkz . Gregoryen takvimine geçiş ).
- Jülyen takvimi (kadar9 Aralık 1582içinde Fransa ). Laik sayı eşittir: 19 eksi yılın ilk iki basamağı.
Örnek : 1200 ila 1299 yılları için seküler sayı 19 - 12 = 7'dir.
- Gregoryen takvimi (o zamandan beri20 Aralık 1582Fransa'da). Aşağıdaki tablo her yüzyıl için laik sayıları vermektedir:
1582 - 1599: 1
1600 - 1699: 0
1700 - 1799: 5
1800 - 1899: 3
1900 - 1999: 1
2000 - 2099: 0
2100 - 2199: 5
Not : Bu sayı, ilk iki hanenin 4'ün katı olduğu durumlar dışında (1600 - 1699, 2000 - 2099) her yüzyılda iki birim azalır.
Yıllık sayı
Aşağıdaki tablo, yıllık sayının 0'a eşit olduğu yılları vermektedir. Bu yıllardan itibaren, yıllık sayı her yıl bir birim, yıl artık yıl ise iki birim artar. Bu tabloyu ezbere öğrenmek istemiyorsak, bu yılların 28 yılda bir (haftanın 7 günü x iki artık yıl arasında 4 yıl) bulunduğunu not edebiliriz.
Yıllık sayısı 0 olan yıllar:| ..04 | ..10 | ||
| ..21 | ..27 | ..32 | ..38 |
| ..49 | ..55 | ..60 | ..66 |
| ..77 | ..83 | ..88 | ..94 |
Örnek : 2012 ve 2016 artık yıllarını saymak gerektiğinden 2010 yılının yıllık sayısı 0 ve 2016 yılının yıllık sayısı 8'dir .
Ayrıca not sonucu, aşağıdaki formül ile verilmektedir bu olabilir: yıl a şu hesaplamayı Öklid bölümü arasında bir (yani 4 numaralı tarafından c biz yazarken a = 4c + r ile, r az 4 hariç) ve Yıllık sayı daha sonra a + c-5'in 7'ye Öklid bölümünün geri kalanı tarafından verilir . Önceki örneklerde şunu buluruz: a = 10 , dolayısıyla c = 2 sonra a + c -5 = 7 , kalanı bölmededir. 7 ile gerçekten 0; ve ikincisi için: a = 16 , dolayısıyla c = 4 , sonra a + c-5 = 15 , 7'ye bölümünden kalan 1'dir; bu aslında 8 modulo 7'ye eşdeğerdir.
Not : İki yılın toplamı aynı seküler sayı + yıllık sayıya sahipse , ilk yılda kullanılan bir Postane takvimi, yalnızca birinin olmadığı durumlar dışında, diğeri için de geçerli olacaktır. bu iki yıldan artık bir yıldır.
Aylık sayı
Aşağıdaki tablo , yılın her ayı için aylık sayıları vermektedir :
| Ay | Aylık sayı |
| Şubat (artık olmayan yıl), Mart, Kasım | 0 |
| Haziran | 1 |
| eylül, aralık | 2 |
| Ocak (artık yıl), Nisan, Temmuz | 3 |
| Ocak (artık olmayan yıl), Ekim | 4 |
| Mayıs | 5 |
| Şubat (artık yıl), Ağustos | 6 |
Örnek : Ocak ayı, 2003'te 4 ve 2004'te (artık yıl) 3 aylık sayıya sahiptir .
Tarih
Son hane tarihin kendisidir, yani aydaki gün sayısıdır.
Örnekler
| Gün | laik sayı | + | yıllık sayı | + | aylık sayı | + | tarih | = | sonuç ( haftanın günü ) |
| 8 Ekim 2003 | 0 | + | 5 | + | 4 | + | 8 | = | 17 = 2x7 + 3 ( Çarşamba ) |
| 9 Aralık 1582 (Jülyen takvimi) | 4 | + | 6 | + | 2 | + | 9 | = | 21 = 3x7 + 0 ( Pazar ) |
| 20 Aralık 1582 (Miladi takvim, ertesi gün 9 Aralık 1582 Fransa'da) | 1 | + | 6 | + | 2 | + | 20 | = | 29 = 4x7 + 1 ( Pazartesi ) |
| 21 Temmuz 1969 | 1 | + | 4 | + | 3 | + | 21 | = | 29 = 4x7 + 1 ( Pazartesi ) |
| Kaç 13. Cuma vardır yılda 2003 ? Aylık sayıyı M ile değiştirerek önceki hesaplamayı yaparsak, aşağıdaki ilaveyi elde ederiz: | |||||||||
| 2003 yılında 13. Cuma | 0 | + | 5 | + | M | + | 13 | = | 5 (Cuma) |
| dolayısıyla M = -13 = 1 - 2x7. Aylık 1 sayısı tek bir Haziran ayına karşılık gelir . | |||||||||
Ezberlenebilir varyant versiyonu (Miladi takvim)
Prensipte bir öncekine benzeyen bu versiyon, zihinsel aritmetiği kolaylaştırmak için hafıza çabasını azaltır. Belirli bir tarih için, aşağıdaki eklemelerin veya birikimlerin sırayla (7'ye bölmede kalanlar korunarak) yapılmasından oluşur:
- Yılın son iki basamağının oluşturduğu sayı ile çeyreğinin tamamının toplamı .
- 6 4 2 ve 0 olarak değerlendirilen seküler bir düzeltme (0 1900'den, 6 2000'den, 4'ten 2100'den, 2'den 2200'den ve yine 0 2300'den ... vb. ve ayrıca takvimin oluşturulduğu 1582 yılından itibaren 0, 6'dan 1600, ...).
- Aşağıdaki 033 614 625 035'e yanıt veren ayın kayması ( Ocak'ta 0, Şubat'ta 3, Aralık'ta 5 ekliyoruz).
- Günün tarihi .
Elde edilen sayı haftanın gününe karşılık gelir: Pazartesi için 1, Salı için 2 ve Pazar için 7 veya 0, bir istisna dışında: artık yılların Ocak ve Şubat aylarında 1 çıkarın (tercihen uygulanır) 1'de, bölme laik istisnalar dışında düştüğünde).
Örnek 1: Hangi gündü 14 Temmuz 1789 ? Yıl 89 ⇒ (70) +19 ⇒ (14) +5 ⇒ 5, çeyreği 22 ⇒ (21) +1 ⇒ 1, yani 5 + 1 = 6 artı yüzyıl ⇒ 4 veya 10⇒3, Temmuz ayı ⇒ 6, dolayısıyla 9 ⇒ 2, tarih (14 ⇒ 0) sonuç 2. Salıydı!
Örnek 2: Hangi gündü 2 Aralık 1804 ? Yıl⇒4 onun çeyreği⇒1, bunların toplamı⇒5, yüzyıl 18⇒2, kümülatif 5 ve 2⇒7⇒0, Aralık⇒5, tarih 2. Bir Pazar günüydü !
Son olarak, ezberlenmesi anlayarak kolaylaştırılabilen yöntemin dışında (tartışmaya bakınız), yapılacak tek bellek çabası, aylık vardiyaların sırasını korumaktan ibarettir.
Şuna da bakın:
İlgili Makaleler
- Takvim
- Gregoryen takvimi ( Gregoryen takvimine geç )
- Jülyen takvimi
- evrensel takvim
- Sabit takvim
- günün belirlenmesi
- Kıyamet Algoritması
Dış bağlantılar
- 1753'ten 2199'a kadar sonsuz takvim
- -3999'dan +3999'a kadar sonsuz takvim, yüklemek için ücretsiz yazılım.
- Yahudi sonsuz takvimi
- Müslüman daimi takvim Miladi takvimden bir tarihin Hicri takvimden bir tarihe dönüştürülmesi.