Hasse diyagramı
Gelen matematik , Hasse diyagramı Alman matematikçisinden adlandırılan, Helmut Hasse , sonlu için görsel bir temsilidir. Bir grafiğin kağıt üzerindeki olağan temsiline benzer şekilde, anlaşılmasını kolaylaştırır.
Hasse diyagramında:
- Sıralı öğeler noktalarla temsil edilir.
- İki öğe arasındaki ilişki, iki nokta arasındaki bir segment ile temsil edilir.
- Bir eleman ise X olan ≤ başka elemanı y , o zaman temsil eden nokta x için daha düşük yerleştirilir y . Bu nedenle, yönlerinin açıklanması için segmentlerin okla işaretlenmesine gerek yoktur.
- Diyagramın aşırı yüklenmesini önlemek için, olası sipariş ilişkilerinin tümü gösterilmemiştir. Geçişli refleksif indirgeme ile sınırlıdırlar:
- Tüm X <y mevcutsa z böyle x <z <y , o zaman kademeli bağlamalıdır x için y .
- Bir elemandan kendisine olan döngüler gösterilmez.
- Mümkün olduğunca segmentleri geçmemeye özen gösteriyoruz.
Sonsuz sıra durumunda, Hasse diyagramını kullanmaya devam edebileceğimizi ve siparişin sonlu bir kısıtlamasını temsil edebileceğimizi unutmayın.
Hasse diyagramı örnekleri
- Bir olan üç on elemanlarının sıralı dizi maksimumları üçü üst sınırlar ve en az elemanının her iki benzersiz alt bağlanan ve alt bağlanan dizi.

- Bölünebilirlik ilişkisine göre sıralanan 60, A = {1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60} bölenler kümesi için, aşağıdaki Hasse diyagramını elde ederiz:

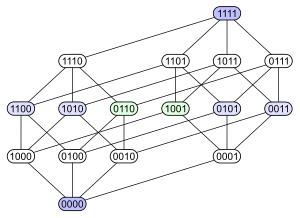
- S = A ∪ B ∪ C ∪ D kümesi, burada A, B, C ve D, S'nin parçalarının olası kombinasyonlarını temsil eden dörtlü Boole'lerdir, öyle ki,
B = { 0100 = {b}, 1100 = {a, b}, 0110 = {b, c}, 0101 = {b, d}, 1110 = {a, b, c}, 1101 = {a, b, d}, 0111 = {b, c, d}, 1111 = {a, b, c, d}}
C = { 0010 = {c}, 1010 = {a, c}, 0110 = {b, c}, 0011 = {c, d}, 1110 = {a, b, c}, 1011 = {a, c, d}, 0111 = {b, c, d}, 1111 = {a, b, c, d}}
D = { 0001 = {d}, 1001 = {a, d}, 0101 = {b, d}, 0011 = {c, d}, 1101 = {a, b, d}, 1011 = {a, c, d}, 0111 = {b, c, d}, 1111 = {a, b, c, d}} S = { 0000 = {}, 1000 = {a}, 0100 = {b}, 0010 = {c}, 0001 = {d}, 1100 = {a, b}, 1010 = {a, c}, 1001 = {a, d}, 0110 = {b, c}, 0101 = {b, d}, 0011 = {c, d}, 1110 = {a, b, c}, 1101 = {a, b, d}, 1011 = {a, c, d}, 0111 = {b, c, d}, 1111 = {a, b, c, d}}
Böylece, dahil etme bağıntısı tarafından sıralanan on altı dördüzden aşağıdaki Hasse diyagramını elde ederiz:
 |
 |
 |

|
Bu dört şeklin hepsi aynı Hasse diyagramını temsil eder, ancak farklı özellikleri göstermek için farklı açılardan:
- İlk diyagram, parça setinin ( S'nin ) kısmen sıralı derecelendirilmiş bir set olduğu gerçeğini gösterir : her bir elemanın ( S'nin parçası ) derecesi , diyagramdaki yüksekliğine karşılık gelir;
- İkinci diyagram da sıra ve yükseklik arasındaki bu uyuşmaya saygı duyar, ancak belirli kenarları gererek tesseraktın geliştirilmesini iki küpün bir birleşimi olarak ekler (boolean dörtlülerini boyut 4'teki koordinatlar olarak yorumlayarak, her biri daha sonra bir tepeye karşılık gelir) hiperküp);
- Üçüncü diyagram, yapının iç simetrisini vurgular;
- Dördüncü diyagram, 4. dereceden bir kare matrisin katsayılarına benzer şekilde düzenlenmiş köşeleri göstermektedir .