Parabolün karesini almak

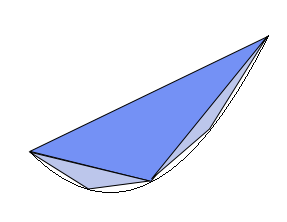
Arşimet alanı hesaplamak için çalışır P a segmenti absis noktaları arasındaki kavisli üçgenin söylemek bir parabol, a ve apsis b , parabol ekseni dikey eksen olan. Daha sonra apsis a , apsis b ve apsis noktalarından geçen bir üçgen çizer . Bu nedenle, P'ye bu büyük üçgenin S alanıyla yaklaşmaya karar verir . Sonra geride bıraktığı küçük eğrisel üçgenlerde yeniden başlar. -de+b2{\ displaystyle {\ dfrac {a + b} {2}}}

Yatay mesafenin ikiye bölündüğünü ve yüksekliğin 4'e bölündüğünü göstererek, her küçük üçgenin alanının büyük üçgenin alanının sekizde birine eşit olduğunu gösterir. P'ye büyük üçgenin ve iki küçük üçgenin alanıyla yaklaşır : sonra, bu şekilde devam ederek, parabol alanına yaklaşır . S+S4{\ displaystyle S + {\ dfrac {S} {4}}}Sdeğil{\ displaystyle S_ {n}}

Sdeğil=S+S4+S16+...+S4değil{\ displaystyle S_ {n} = S + {\ dfrac {S} {4}} + {\ dfrac {S} {16}} + ... + {\ dfrac {S} {4 ^ {n}}} }

Bu zamandan itibaren yazılabileceğini biliyoruzSdeğil{\ displaystyle S_ {n}}

Sdeğil=43S-13S4değil{\ displaystyle S_ {n} = {\ dfrac {4} {3}} S - {\ dfrac {1} {3}} {\ dfrac {S} {4 ^ {n}}}}

ama sınıra nasıl gideceğimizi bilmiyoruz. Sadece Arşimet'in bu şekilde çağırdığı tükenme ilkesini nasıl kullanacağımızı biliyoruz .

Teorem  -  Bu, [parabolün] bu bölümüne, kalan bölümlerin herhangi bir verili alandan daha küçük olacak şekilde bir çokgeni yazmanın mümkün olduğunu göstermiştir; çünkü bu önermeden dolayı [segmentin] yarısından daha büyük olan bir alanı daima çıkararak, kalan segmentleri azaltmaya devam ederek [bir zaman gelecek] onları daha az yapacağımız açıktır. herhangi bir alan.

Bu ilke Kitabı Önerme 1 bulunursa X arasında Elements Öklid ve dayanmaktadır Arşimed ' aksiyomuna .

Arşimet daha sonra P'nin büyük ve P'nin küçük olmasının saçma olduğunu gösterir . 43S{\ displaystyle {\ dfrac {4} {3}} S}43S{\ displaystyle {\ dfrac {4} {3}} S}

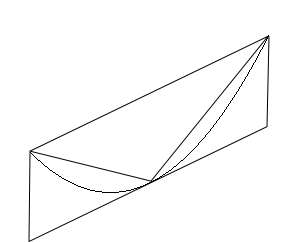
• P'nin büyük olduğunu varsayalım . 43S{\ displaystyle {\ dfrac {4} {3}} S}P ile arasındaki farkın istendiği kadar küçültülebileceğini gösteriyor. Aslında, parabolün alanından, parabol alanının yarısından fazlasını temsil eden üçgenin alanını çıkarıyoruz çünkü üçgenin alanı, çizilen paralelkenar, parabolün alanından daha büyük alan. Ve böylece her adımda. Böylece onu daha küçük yapabilir . Bu , daha büyük olduğu anlamına gelir . İfadesine göre saçmadır .Sdeğil{\ displaystyle S_ {n}}P-Sdeğil{\ displaystyle P-S_ {n}}P-43S{\ displaystyle P - {\ dfrac {4} {3}} S}Sdeğil{\ displaystyle S_ {n}}43S{\ displaystyle {\ dfrac {4} {3}} S}Sdeğil{\ displaystyle S_ {n}}

• Varsayalım ki P azdır . 43S{\ displaystyle {\ dfrac {4} {3}} S}Aynı tükenme ilkesine göre, farkı istediğimiz kadar küçük yapabiliriz , çünkü her adımda geriye kalanların 3 / 4'ünü çıkarırız. Bu nedenle daha küçük alabiliriz . Bu, P'den daha büyük olduğu anlamına gelir . Üçgenler parabol segmentinin içinde olduğu için bu saçmadır.43S-Sdeğil{\ displaystyle {\ dfrac {4} {3}} S-S_ {n}}43S-P{\ displaystyle {\ dfrac {4} {3}} SP}Sdeğil{\ displaystyle S_ {n}}

İki dava ortadan kaldırılır, Arşimet bu sonuca varır . P=43S{\ displaystyle P = {\ dfrac {4} {3}} S}

“Herhangi bir alandan daha az” ifadesinin Arşimet'in kullanmadığı sınır kavramına çok yakın olması ilginçtir. Bu nedenle, eşitliğini kanıtlamak için kendini saçma bir şekilde düşünmeye zorladı.

Yöntem , mülkü üç adımda gösteren Arapça konuşan matematikçi İbrahim ibn Sinan tarafından ele alınacak . İlk olarak, bir afinitenin çokgenlerin alan oranlarını koruduğunu gösterir. Ardından, iki parabol bölümünün alanlarının oranının, ilişkili üçgenlerin alanlarının oranına eşit olduğunu kanıtlamak için tükenme yöntemini uygulayan gösterisinin kalbi geliyor. Akıl yürütmenin sonu çok hızlıdır: bir parabol ve onunla ilişkili üçgeni çizerek, parabolün alanının , parabollerin kalan bölümlerinin iki alanını eklediğimiz ilişkili üçgenin alanına eşit olduğunu fark eder. . Parabollerin bu kısımlarıyla ilişkili üçgenlerin ilk üçgenin alanının 1 / 8'i kadar bir alana sahip olduğunu gösterir. Bundan parabol kısımlarının alanlarının oranı için aynı olduğunu çıkarır ve böylece elde eder. ATp{\ displaystyle A_ {p}}ATt{\ displaystyle A_ {t}}ATp′{\ displaystyle A_ {p '}}

ATp=ATt+28ATp{\ displaystyle A_ {p} = A_ {t} + {\ frac {2} {8}} A_ {p}}

Ya da yine: . ATp=43ATt{\ displaystyle A_ {p} = {\ frac {4} {3}} A_ {t}}

Tartım yöntemi

Arşimet, aynı çalışmada, mekanik dehasını ortaya koyan kareyi tartarak bir sunum sunar. İlke, 1906'da bir palimpsestte keşfedilen Arşimet'in metninin benzersiz bir el yazmasında detaylandırılmıştır. La Quadrature de la parabole adlı incelemesinde , tükenme yöntemini kullanarak muhakemesini tamamlar .

Bir kaldıraç sistemi kullanarak parabolü tartmaya karar verir .

Burada sunulan şekil, Arşimet'in çalışmasında görülenlerin basitleştirmesidir. Doğru (AC), A'da parabole teğettir, segment [BC] parabolün eksenine paraleldir. [AB] 'nin ortasında parabolün eksenine paralel D noktası projelendirir.

Buradaki fikir, ağırlık merkezinde G asılı duran ABC üçgenini, A 'noktasına yerleştirilen bir kütle ile dengelemektir.

Arşimet bölümlere göre ilerler. Hg'de askıya alınmış ABC üçgeni, H.'de askıya alınmış çok sayıda MP parçası ile değiştirilebilir. Arşimet, MN'nin MP için BM'nin BA için ne olduğunu çoktan göstermiştir (parabollerde işlenmiştir). Şimdi şöyle görünüyor:

MDEĞİLMP=BMBAT{\ displaystyle {\ dfrac {MN} {MP}} = {\ dfrac {BM} {BA}}}

Sayesinde Thales teoremi , biz de eşitlik var

BMBAT=ÖHÖAT{\ displaystyle {\ dfrac {BM} {BA}} = {\ dfrac {OH} {OA}}}

Bu nedenle

MDEĞİLMP=ÖHÖAT=ÖHÖAT′{\ displaystyle {\ dfrac {MN} {MP}} = {\ dfrac {OH} {OA}} = {\ dfrac {OH} {OA '}}}

Sonra:

ÖH×MP=ÖAT′×MDEĞİL{\ displaystyle OH \ times MP = OA '\ times MN}

A 'içerisine yerleştirilen [MN] bölücü böylelikle H'ye yerleştirilmiş parçayı [MP] dengeler.

Böylelikle bölüme göre bölümlere ayırarak, A 'içine yerleştirilmiş parabol bölümüyle Hg'ye yerleştirilmiş ABC üçgenini dengeler. Bu nedenle

×{\ displaystyle \ times}

×{\ displaystyle \ times}

Gibi , elimizdeki ÖHg=13ÖAT{\ displaystyle OHg = {\ dfrac {1} {3}} OA}

13{\ displaystyle {\ dfrac {1} {3}}}

Son olarak, benzetmeler üzerine yapılan aynı incelemede Arşimet, ABC'nin alanının ABD'nin 4 katı olduğunu zaten göstermiştir.

Parabolün alanı bu nedenle ABD üçgeninin alanına eşittir . 43{\ displaystyle {\ dfrac {4} {3}}}

Ardışık Tamsayılar İçin Kareler Toplamı Formülünü Kullanma

Bu yöntem, tüm "parabol çeşitlerinin" karesini almak için ardışık tam sayıların toplamlarının kullanılmasından oluşur . Parabol kısmında veya parabolün altındaki yüzeyde, alanı tam sayıların karesiyle orantılı olan dikdörtgenlerin veya yamukların kesilmesinden oluşur. Bu yöntem ile geliştirilmiştir Blaise Pascal onun içinde Potestam numericarum Summa kullanır (1654) indivisibles yöntemi ile daha sonra John Wallis aynı zamanda onun herhangi bir pozitif rasyonel üs onu genişletir 1656 yılında Arithmetica infinitorum .

Pascal ve Wallis [0, a ] aralığında parabolün altındaki alanı hesaplar . Parabol kısmının alanı daha sonra tamamlayıcılıkla belirlenebilir.

Apsis 0 ve a noktaları arasındaki parabolün altındaki alanı hesaplamak için , [0, a] aralığını aynı d boyutundaki n aralığına bölerek apsisleri vurgularız . Aralığı içinde, parabol altındaki alan baz d ve yükseklikleri olan dikdörtgenleri alanı arasında olan ve . xk,değil=-dekdeğil{\ displaystyle x_ {k, n} = a {\ frac {k} {n}}}[xk,değil,xk+1,değil]{\ displaystyle [x_ {k, n}, x_ {k + 1, n}]}xk,değil2{\ displaystyle x_ {k, n} ^ {2}}xk+1,değil2{\ displaystyle x_ {k + 1, n} ^ {2}}

Özetle eşitsizliğe ulaşıyoruz:

d∑k=0değil-1xk,değil2≤ATp≤d∑k=1değilxk,değil2,{\ displaystyle d \ toplamı _ {k = 0} ^ {n-1} x_ {k, n} ^ {2} \ leq A_ {p} \ leq d \ toplamı _ {k = 1} ^ {n} x_ {k, n} ^ {2},}

sakin ol

-de3değil3(02+12+22+⋯+(değil-1)2)≤ATp≤-de3değil3(12+22+⋯+değil2).{\ displaystyle {\ frac {a ^ {3}} {n ^ {3}}} (0 ^ {2} + 1 ^ {2} + 2 ^ {2} + \ cdots + (n-1) ^ { 2}) \ leq A_ {p} \ leq {\ frac {a ^ {3}} {n ^ {3}}} (1 ^ {2} + 2 ^ {2} + \ cdots + n ^ {2} ).}

Ardışık karelerin toplamına ilişkin formül

12+22+⋯+değil2=değil(değil+1)(2değil+1)6,{\ displaystyle 1 ^ {2} + 2 ^ {2} + \ cdots + n ^ {2} = {\ frac {n (n + 1) (2n + 1)} {6}}}

ve sınıra bir geçiş, sonuca varmayı mümkün kılar.

-de3değil3değil(değil-1)(2değil-1)6≤ATp≤-de3değil3değil(değil+1)(2değil+1)6.{\ displaystyle {\ frac {a ^ {3}} {n ^ {3}}} {\ frac {n (n-1) (2n-1)} {6}} \ leq A_ {p} \ leq { \ frac {a ^ {3}} {n ^ {3}}} {\ frac {n (n + 1) (2n + 1)} {6}}.}

ATp=-de33.{\ displaystyle A_ {p} = {\ frac {a ^ {3}} {3}}.}

Benzer bir yaklaşım, zaten sırasında kurulmuştu IX inci  yüzyılın tarafından Sabit bin Kurra görünüşe göre, Arşimet Antlaşması'nı bilmiyordu ve böylelikle kendi yöntemlerini geliştirmek zorunda kaldı. Thābit ibn Qurra , yükseklikleri sabit olmayan ancak yamukların alanları tek tamsayıların kareleriyle orantılı olacak şekilde inşa edilen parabol yamuklarının kendi bölümünde kayar. Metodu, 0 ile b arasında tabanları koordinatları olan yamuklar dahil olmak üzere denklem parabolünün kısmında kesip çıkarmaktan ibarettir . Bu şekilde oluşturulan yamukların yüksekliği y=x2{\ displaystyle y = x ^ {2}}yk,değil=bk2değil2{\ displaystyle y_ {k, n} = b {\ frac {k ^ {2}} {n ^ {2}}}}

hk,değil=b((k+1)2değil2-k2değil2)=b2k+1değil2{\ displaystyle h_ {k, n} = b \ sol ({\ frac {(k + 1) ^ {2}} {n ^ {2}}} - {\ frac {k ^ {2}} {n ^ {2}}} \ sağ) = b {\ frac {2k + 1} {n ^ {2}}}}

ve üsler için

2k+1değilb{\ displaystyle 2 {\ frac {k + 1} {n}} {\ sqrt {b}}}

2kdeğilb{\ displaystyle 2 {\ frac {k} {n}} {\ sqrt {b}}}

Parabol kısmının alanı bu nedenle yamukların alanlarının toplamı ile yaklaşık olarak hesaplanır, yani

Sdeğil=bb1değil3∑k=0değil-1(2k+1)2=bbdeğil(4değil2-1)/3değil3{\ displaystyle S_ {n} = b {\ sqrt {b}} {\ frac {1} {n ^ {3}}} \ toplamı _ {k = 0} ^ {n-1} (2k + 1) ^ {2} = b {\ sqrt {b}} {\ frac {n (4n ^ {2} -1) / 3} {n ^ {3}}}}

Bir tükenme yöntemiyle (bugün sınıra gideceğiz) daha sonra parabol bölümünün alanının ilişkili üçgenin alanının 4 / 3'üne eşit olduğunu kanıtlar.

Geometrik dizilerin kullanımı

Bu yöntem, 1636'da Fermat tarafından kuruldu ve daha sonra parabol ve hiperbol olarak adlandırdığı ve gerçekte güç fonksiyonlarının eğrileri olan alanı hesaplamak için genelleştirildi (tamsayı, pozitif, negatif veya 1 / n , 1'den farklı). Prensip, kare alınacak yüzeyin altındaki boşluğu geometrik bir ilerlemeye göre kesmekten ibarettir . Eğrinin altındaki alana daha sonra bu bölme ile elde edilen dikdörtgenlerin alanı tarafından yaklaşılır; bu alanlar da geometrik ilerleme içindedir. Sınıra çift geçişle (geometrik dizinin sınırı, ardından dizinin nedeni 1'e yaklaştığında sınırla), aranan yüzeyin alanını buluruz.

Mevcut gösterimlerde, [0, a] aralığında denklemin yarı-parabolü üzerinde gösterilebilir: [0, a] aralığının, r nedeninin geometrik ilerlemesine göre bölünmesi, x koordinatlarını vurgular . Aralık boyunca, eğrinin altındaki alan temel dikdörtgenlerin alanı arasındadır. y2=x{\ displaystyle y ^ {2} = x}xk,r=-derk{\ displaystyle x_ {k, r} = ar ^ {k}}[xk+1,r,xk,r]{\ displaystyle [x_ {k + 1, r}, x_ {k, r}]}

dk,r=-de(rk-rk+1)=-de(1-r)rk{\ displaystyle d_ {k, r} = a (r ^ {k} -r ^ {k + 1}) = a (1-r) r ^ {k}}

ve yükseklikler

hk,r=-de1/2rk/2{\ displaystyle h_ {k, r} = a ^ {1/2} r ^ {k / 2}}

hk+1,r=r1/2hk,r{\ displaystyle h_ {k + 1, r} = r ^ {1/2} h_ {k, r}}

Özetle eşitsizliğe ulaşıyoruz

-de3/2(1-r)r1/2∑k=0değil-1r3k/2≤ATdeğil≤-de3/2(1-r)∑k=0değil-1r3k/2{\ displaystyle a ^ {3/2} (1-r) r ^ {1/2} \ toplamı _ {k = 0} ^ {n-1} r ^ {3k / 2} \ leq A_ {n} \ leq a ^ {3/2} (1-r) \ toplam _ {k = 0} ^ {n-1} r ^ {3k / 2}}

aralık üzerinde parabolün altındaki alan nerede . Geometrik mantık dizisindeki sınıra geçerek , çerçevelemeyi elde ederiz. ATdeğil{\ displaystyle A_ {n}}[xdeğil,r,-de]{\ displaystyle [x_ {n, r}, a]}r3/2{\ displaystyle r ^ {3/2}}

-de3/2(1-r)r1/211-r3/2≤AT≤-de3/2(1-r)11-r3/2{\ displaystyle a ^ {3/2} (1-r) r ^ {1/2} {\ frac {1} {1-r ^ {3/2}}} \ leq A \ leq a ^ {3 / 2} (1-r) {\ frac {1} {1-r ^ {3/2}}}}

sonra basitleştirme ile 1-r1/2{\ displaystyle 1-r ^ {1/2}}

-de3/2r1/21+r1/21+r1/2+r≤AT≤-de3/21+r1/21+r1/2+r.{\ displaystyle a ^ {3/2} r ^ {1/2} {\ frac {1 + r ^ {1/2}} {1 + r ^ {1/2} + r}} \ leq A \ leq a ^ {3/2} {\ frac {1 + r ^ {1/2}} {1 + r ^ {1/2} + r}}.}

1 e eğilimi için limite ikinci bir geçiş eşitliği verir

AT=23-de3/2{\ displaystyle A = {\ frac {2} {3}} a ^ {3/2}}

Parabol yarım parçasının alanı, onu içeren dikdörtgenin 2 / 3'üne eşittir.

Bu teknik, herhangi bir denklem eğrisine genelleştirilir , gerçek α -1'den farklıdır, eğrinin altındaki alanı [0, a] eğer α> -1 ise veya [a; + ∞ [eğer α <-1 y=xα{\ displaystyle y = x ^ {\ alpha}}

Integral hesabı

[0, a ] aralığı boyunca parabolün altındaki alan , integrale karşılık gelir

∫0-dex2dx.{\ displaystyle \ int _ {0} ^ {a} x ^ {2} \ mathrm {d} x.}

Analizin temel teoremi bir antitürevi bu integrali bağlantı sağlayan F arasında kare fonksiyonu

∫0-dex2dx=F(-de)-F(0){\ displaystyle \ int _ {0} ^ {a} x ^ {2} \ mathrm {d} x = F (a) -F (0)}

Bir ilkel tablo , kare fonksiyonunun bir ilkelinin belirlenmesini mümkün kılar: ve beklenen sonucu sağlar. F(x)=x33{\ displaystyle F (x) = {\ frac {x ^ {3}} {3}}}

Notlar ve referanslar

Notlar

1. Yani y = kx n denkleminin tüm eğrileri .
2. Pascal ve Wallis, dikdörtgenler yerine eşit aralıklı çizgiler üzerinde çalışmayı içeren bölünmez yöntemini kullanır .
3. Bu aynı örnek de Fermat tarafından ancak bu çok uzak bir kelime ile işlenir XX inci  yüzyıl, bkz Pierre de Fermat'ı Jules Tabakhane ve Charles Henry , Fermat'ın Works , vol.  3,1896( çevrimiçi okuyun ) , s.  216 ve sonrası.

Referanslar

1. (fr + grc) Arşimet, La quadrature de la parabole , Paris, Les Belles Lettres ,1971( ISBN  2-251-00025-9 ) , sayfa 189.
2. Rüşdi Raşid ve Hélène Bellosta , İbrahim ibn Sinan, mantık ve geometri X inci  yüzyıl , Brill,2000( çevrimiçi okuyun ) , s.  229-244.
3. Jean-Louis Gardies , Pascal entre Eudoxe et Cantor ( çevrimiçi okuyun ) , s.  62.
4. (in) Jacqueline Stedall , "  Harikaların keşfi: John Wallis'in Arithmetica infinitorum'unun satır aralarını okumak  " , Arch. Geçmiş Exact Sci. , cilt.  56, n o  1,2001, s.  1-28 ( DOI  10.1007 / s004070100040 ).
5. (inç) John Wallis, Arithmetica infinitorum , XIX - XXIV arası öneriler .
6. (in) Rüşdi Raşid ve Regis Morelon , Arapça Bilim Tarihi Ansiklopedisi , vol.  2, Routledge ,1996( çevrimiçi okuyun ) , s.  421.
7. Stoll 1993 , s.  55.
8. Dahan ve Peiffer , s.  182.

Kaynakça

• A. Dahan-Dalmedico ve J. Peiffer , Matematik A History: Yollar ve Labirent ile ,1986[ basımların ayrıntıları ]
• Roshdi Raşid , son derece küçük matematik IX inci için XI inci  yüzyılda , vol.  1, Londra, Al-Furqan İslami Miras Vakfı,1996
• André Stoll , "  Matematik tarihi, integral hesaba olası bir yaklaşımı nasıl ortaya çıkarabilir  ", Repères-IREM , n o  11,Nisan 1993( çevrimiçi okuyun )
• Tarihte matematiksel gösteri , IREM de Lyon
• [PDF] Parabolün karesini alma
• [PDF] Tartım yöntemine göre kareleme , matematik semineri, IUFM de La Réunion